Capital As Power

Tag: terms of trade

  • Problems of the Periphery in Federico and Tena’s World Trade Data

    Problems of the Periphery in Federico and Tena’s World Trade Data

    Originally published at joefrancis.info

    Joe Francis

    Giovanni Federico and Antonio Tena-Junguito (2016) have produced a data set of world trade that includes exports and imports, in both current and constant prices, going back to the early nineteenth century for over 100 countries. It will give all economic historians a mass of easily available long-term time series. What could there possibly be to complain about? In short, methodologically speaking, it’s a bit iffy.

    In an article published in Historical Methods I showed that any attempt to measure a peripheral country’s terms of trade during the nineteenth century using prices taken from the core countries will have a downward bias in its trend due to the effects of price convergence (Francis 2015). It appears, however, that Federico and Tena may not have read that article.

    Federico and Tena’s goal is to produce export and import values in both current and constant values for all the countries in their sample. Their general approach appears to be to find the current values then deflate them using price indices. When possible, those indices are calculated using prices from the countries themselves, but for peripheral countries they more often than not have to construct new indices by taking prices from Britain, then subtracting freight and insurance rates, in order to arrive at estimates of the export price in the country of origin. For that country’s imports, the procedure is done in reverse: freight and insurance are added to British prices.

    The problem with this methodology is that trade costs included far more than freight and insurance. The clue is in the term ‘cost, insurance, and freight’ (CIF). CIF prices include not only insurance and freight but also other costs, which would need to be subtracted to arrive at ‘free on board’ (FOB) prices or added to FOB prices to arrive at CIF prices. By only subtracting or adding freight and insurance, Federico and Tena ignore the substantial other costs that accounted for the majority of international price differences during the nineteenth century.

    The price of US cotton in Britain illustrates the problem with Federico and Tena’s methodology. Figure 1 shows that in the 1820s US cotton cost 3-8 cents more per pound in Britain than in the United States. Of this difference, around half a cent was due to freight and even less due to insurance. The remainder was due to other costs. Consequently, subtracting freight and insurance from the British price is not enough to arrive at the US price. As shown in Figure 2, the estimated price is substantially too high early in the nineteenth century, although the gap then lowers. This is confirmed by Figure 3, which shows the actual price as a percentage of the estimated price. For the late 1810s, it is around 70 per cent, and then rises to less than 10 per cent by the 1890s. Federico and Tena’s methodology thus tends to overestimate the prices of a country’s exports (and underestimate the prices of its imports) for the early nineteenth century.

    There are at least two implications of this finding. Firstly, when Federico and Tena use their estimated price indices to deflate current export values, they will tend to overestimate the growth in volume, while they will underestimate the growth in import volumes. Secondly, Federico and Tena’s data should not be used to calculate the terms of trade for any country for which they have used this kind of price series.

    Going forward, it does not seem fruitful to continue trying to correct prices from the core countries to estimate prices in peripheral countries because it is hard to say exactly what the other trade costs were. David Jacks has suggested they should include ‘storage costs, tariffs, taxes, and spoilage’, as well as ‘exchange rate risk, prevailing interest rates, and/or the risk aversion of agents’ (Jacks 2005, 401–2, fn. 1). As if that wasn’t complicated enough, they should also probably include the markup of the merchants doing the importing and exporting. Taking wild guesses at what these costs would have been early in the nineteenth century is unwise. Instead, prices from the peripheral countries themselves are needed, so researchers need to get to work reconstructing peripheral countries’s price histories rather than relying upon price data from the core countries.

    References

    Carter, S.B. et al, eds., Historical Statistics of the United States: Earliest Times to the Present: Millennial Edition, New York, 2006, Series Ee618, available online at http:/ /hsus.cambridge.org/HSUSWeb/HSUSEntryServlet (accessed 20 November 2013).

    Francis, J.A. (2015) ‘The Periphery’s Terms of Trade in the Nineteenth Century: A Methodological Problem Revisited’, Historical Methods, 48:1, pp. 52-65.

    Federico, G. and A. Tena-Junguito (2016) ‘World Trade, 1800-1938: A New Data-Set’, Working Papers in Economic History, Universidad Carlos III de Madrid.

    Jacks, D. (2005) ‘Intra- and International Commodity Market Integration in the Atlantic Economy, 1800–1913’, Explorations in Economic History, 42, pp. 381–413.

    Simon, M. (1960) ‘The United States Balance of Payments, 1861–1900’, in Conference on Research in Income and Wealth, Trends in the American Economy in the Nineteenth Century, Princeton, pp. 629-715.

  • Jeffrey Williamson’s Terms of Trade

    Jeffrey Williamson’s Terms of Trade

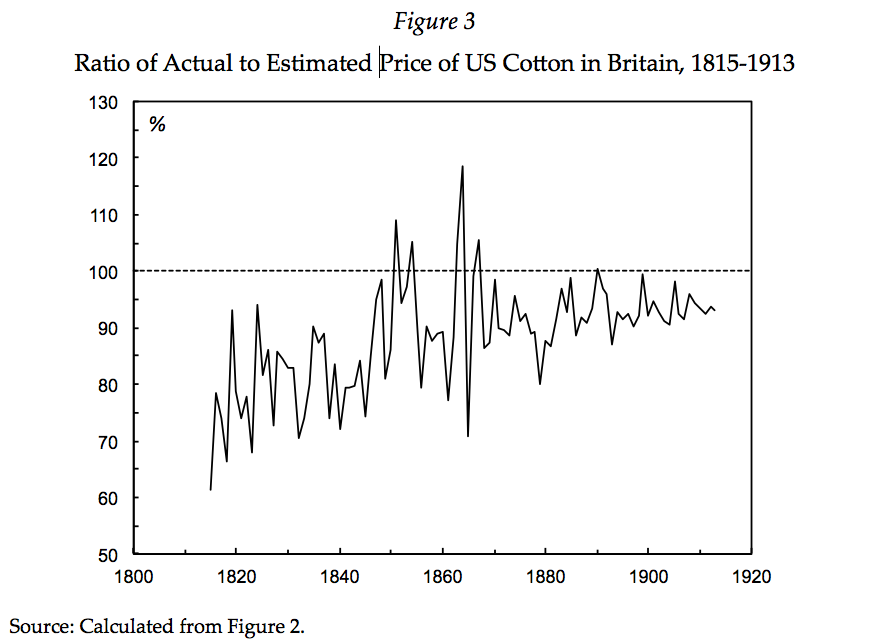
    Originally published at joefrancis.info

    Joe Francis

    Jeffrey Williamson‘s (2011) book Trade and Poverty: When the Third World Fell Behind is one of the most interesting attempts to explain the ‘great divergence’ between rich and poor countries. It is a shame, then, that it is marred by his use of Mickey Mouse numbers.

    In simplified terms, Williamson argues that a long terms-of-trade boom made the periphery deindustrialise in the nineteenth century. Improved terms of trade undercut import-competing proto-industrial sectors, while capital and labour instead focused on primary-commodity production for export.

    According to Williamson, specialisation led to the great divergence because (1) ‘industrial-urban activities contain far more cost-reducing and productivity-enhancing forces than do traditional agriculture and traditional services’ (2011, p. 49); (2) specialisation led to a ‘resource curse’ that saw the periphery’s institutions come to reflect the interests of the rent-seeking elites that were the principal beneficiaries of primary-commodity exports (2011, pp. 50-51); and (3) there was more growth-inhibiting volatility because primary-commodity prices fluctuate more dramatically than those of manufactured goods (2011, pp. 51-53). Williamson’s new narrative thus has the long terms-of-trade boom generating divergence by dividing the world into an industrialised core and a poor, deindustrialised periphery that was afflicted by bad institutions and great instability.

    Williamson (2008) supports his narrative with a data set of the terms of trade of numerous peripheral countries. This empirical aspect of his work has been widely applauded. One prominent reviewer, for example, states that a ‘major contribution of Williamson’s research is the compilation of a data set on the terms of trade for 21 poor countries’ (Crafts 2013, p. F193). Yet, as will be seen in this post, this data set should not be taken seriously.

    The problems with the periphery’s terms-of-trade data is that there are few price data for the peripheral countries themselves, so prices from the core countries must be used as proxies. These prices will be misleading to the extent that trade costs between the core and periphery change. Figure 1, for example, provides a notional illustration of what happens when trade costs fall. The prices of a country’s exports in the importing country drop, even as they rise at home. At the same time, the prices of its imports rise in the exporting country, even as the prices fall at home. Hence, any terms of trade calculated using the other country’s prices will have a downward bias in the trend.

    Figure 1: Prices of an Internationally-Traded Good with Falling Trade Costs

    International-prices

    Note: The figure shows the notional price of an internationally-traded good. It shows how falling trade costs can mean that the domestic price of a country’s exports can go up, even as the price of that same good falls in the importing country.

    WIlliamson (2011, p. 29) himself is aware of this problem. He describes the ‘ideal measure’ of a country’s terms of trade as being calculated using its own prices, whereas the ‘worst-case scenario’ uses prices from other countries. Williamson claims, however, that the problem does not seriously affect his data set. He writes:

    ‘Having pointed out the flaws in the worst-case scenario, it should be stressed that there are only 6 of these (out of 21) [in his data set]. The other 15 are taken from country-specific sources and do an excellent job in constructing estimates that come close to the ideal measure […]’. (Williamson 2011, p. 29)

    To check this claim, I examined the sources for all 21 of Williamson’s series as part of my doctoral research. I found that only two were calculated following Williamson’s ‘ideal measure’ – that is, using prices from the peripheral countries themselves. By contrast, fully 12 were constructed entirely from prices from the core countries; three used core prices for imports; two used core prices that were adjusted for changes in transportation costs; the final two appeared to be of little value because their sources were dubious (see Francis 2013, Appendix 2.1).

    Williamson’s claim about the quality of his data therefore seems misleading to say the least. Why this matters can be seen in Figure 2. Here, what Williamson calls the ‘ideal measure’ estimates (the thick lines) are compared with the ‘worst-case scenario’ estimates (the thin lines). The result clearly shows the downward bias in the trend of the latter. Indeed, in four out of six cases the ‘worst-case scenario’ terms of trade have a downward, whereas the ‘ideal measure’ has an upward trend. It is difficult, therefore, to take his data set seriously.

    Figure 2: Terms of Trade, 1860s-1913

    ToTs for 6 countries

    Note: The thick lines are what Williamson calls ‘ideal measure’ terms of trade, the thin lines are ‘worst-case scenario’ terms of trade. The annual trends are calculated as the rate of change of the exponential trend line. Sources: Ho (1930); Taylor and Michel (1931, pp. 18-19); Hou (1965, pp. 194-98); Glazier, Bandera, and Berner (1975, pp. 30-33, Table 5); Yamazawa and Yamamoto (1979, pp. 169-70, 193, 197); Korthals Altes (1994, pp. 158-60); data underlying Blattman, Hwang, and Williamson (2007), available online; data underlying Williamson (2008), kindly provided by Professor Williamson; Federico and Vasta (2009, pp. 22-23, Table 2).

    Given these flaws in Williamson’s data set, some of his results must be rejected as unreliable. Most notably, in Chapter 11, which draws on an earlier article by Christopher Blattman, Jason Hwang, and Williamson (2007), the dubious terms-of-trade estimates are fed into econometric models to demonstrate the ‘globalisation and great divergence connection’. My research into WIlliamson’s data suggests that none of the results reported in that chapter can be relied upon, although it is important to note that my findings strongly reinforce his core narrative, as they indicate that the periphery’s terms-of-trade boom was considerably greater that he has suggested.

    References

    Blattman, C., J. Hwang, and J.G. Williamson, ‘Winners and Losers in the Commodity Lottery: The Impact of Terms of Trade Growth and Volatility in the Periphery 1870-1939’, Journal of Development Economics, 82:1, 2007, pp. 156-79.

    Crafts, N.F.R., ‘Book Review Feature: Trade and Poverty: When the Third World Fell Behind’, Economic Journal, 123, 2013, pp. F193-97.

    Federico, G., and M. Vasta, ‘Was Industrialization an Escape from the Commodity Lottery? Evidence from Italy, 1861-1940’, Dipartimento di Economia Politica Quaderno 573, Università degli Studi di Siena, 2009.

    Francis, J.A., ‘The Terms of Trade and the Rise of Argentina in the Long Nineteenth Century’, PhD diss., London School of Economics and Political Science, 2013.

    Glazier, I.A., V.N. Bandera, and R.B. Berner, ‘Terms of Trade Between Italy and the United Kingdom 1815–1913’, Journal of European Economic History, 4:1, 1975, pp. 5-48.

    Ho, F.L., Index Numbers of the Quantities and Prices of Imports and Exports and of the Barter Terms of Trade in China, 1867-1928, Tientsin, 1930.

    Hou, C., Foreign Investment and Economic Development in China 1840-1937, Cambridge, MA, 1965.

    Korthals Altes, W.L., Changing Economy in Indonesia: A Selection of Statistical Source Material from the Early 19th Century up to 1940, XV, Prices (Non-Rice) 1814–1940, Amsterdam, 1994.

    Taylor, K.W., and H. Michel, Statistical Contributions to Canadian Economic History, II, Toronto, 1931.

    Williamson, J.G., ‘Globalization and the Great Divergence: Terms of Trade Booms, Volatility and the Poor Periphery, 1782-1913’, European Review of Economic History, 12:3, 2008, pp. 355-91.

    _____, Trade and Poverty: When the Third World Fell Behind, Cambridge, MA, 2011.

    Yamazawa, I., and Y. Yamamoto, Estimates of Long-Term Economic Statistics of Japan since 1868, XIV, Foreign Trade and Balance of Payments, Tokyo, 1979.