- This topic has 9 replies, 4 voices, and was last updated December 24, 2021 at 7:10 pm by .
-
Topic
-
by Shimshon Bichler & Jonathan Nitzan
First posted as a Research Note
Immortality
This note offers some speculative ideas worth considering. One of the key features of all hierarchical civilizations is their rulers’ fear of death. This fear was famously narrated in the ancient myth of Gilgamesh – the Sumerian king who realized that, like all other humans, he too was destined to die and embarked on a desperate quest to annul his mortality (Mitchell 2004; Kramer 1956). According to Lewis Mumford (1967, 1970), this quest for immortality is the main reason why society’s rulers are forever obsessed with building and fortifying power hierarchies – or ‘megamachines’, as he called them. Controlling these megamachines, Mumford argued, is the rulers’ way of playing God, a futile yet all-possessive effort to conquer the future and live forever.
Capitalist Immortality
In capitalism, the rulers finally figured out how to do it – sort of. Like their predecessors, capitalists too are obsessed with their mortality, and they too build hierarchical megamachines – the most powerful ever – to quell this obsession. But their megamachines are fundamentally different. Unlike prior versions, theirs are governed by a single, universal ritual – capitalization – and this ritual focuses explicitly and solely on the future. Technically, capitalization pretends to compress the entire future to the here-and-now: it encourages owners to bring – or ‘discount’, in their lingo – everything in the future that affects earnings back to the current moment; it allows them to give the result a definitive dollar quantity; and its permits them to label the outcome ‘present value’.
No previous mode of power came even close to this majestic achievement. In the past, most promises to pay were postponed to the afterlife, sans guarantee. Not so in capitalism. The future remains unknowable, of course, but in capitalism the rulers bypass this hassle by pretending to predict what lies ahead with statistical measures of certainty. This pretention makes the future, for the first time ever, appear wholly ownable. Nowadays, capitalists don’t have to wait for the uncertain afterlife or Karma-like incarnation to reap their promised gains. They already own all these gains here and now, quantified in the universally discounted units of market capitalization. And because for capitalists, ownership is life, the fact that they own the entire future of earnings – including the earnings of their assets’ subsequent owners – makes them immortal right now. This self-deceptive ploy must be the most glorious, effective and all-encompassing con job ever.
The Capitalist Degree of Immortality
As with all con jobs, though, this one too comes with tricky fine prints. In order to capitalize the future, you must first know it, and as we all know, the future is unknowable, even to know-all capitalists. Moreover, the future is very long, some say infinite. And since, as finance guru Benjamin Graham dictates, capitalization should discount the future ‘all the way to eternity’ (quoted in Zweig 2009: 28), it is impossible for anyone – capitalists included – to see it all. In this sense, no one, not even the most farsighted capitalist, can ever be fully immortal.
Instead, each capitalist has his or her own ‘degree of immortality’, depending on how far they can look ahead. All else remaining the same, those who see farther achieve greater immortality, whereas those whose vision is more impaired must settle for less. In capitalism, even eternal life is differential.
The degree of immortality is easy to measure, at least in principle. In finance, the ‘true value’ of an asset is defined as the discounted, or present value of its future earnings. [2] If these earnings are known, ‘true value’ at any time t is given by their capitalization Kt as shown in Equation 1:
where Et+i is the earnings in period t+i, for any i=1 to n, and r is the discount rate at time t.
In practice, this equation can look messy, since it requires specifying the earnings received in each and every period. We can make it neater, though, by starting from the current level of earning Et and finding the compounded earning growth rate g that will yield the same capitalization given by Equation 1, such that:
Finally, if the earnings being capitalized continue to flow indefinitely, and if (r > g), Equation 2 becomes even simpler:
And that’s all we need for our calculations. Capitalists can achieve immortality here and now only by accurately discounting all their future earnings. And if earnings continue to flow forever, they need to use Equation 3 to capitalize them. Actual capitalists, though, can see only part of the future, which means that even if their partial projections are accurate, they can use only the less accurate Equation 2 (which covers only the n periods they can predict), instead of Equation 3 (which requires knowing all earnings to infinity).
Expressing the partial capitalization of Equation 2 as a per cent of the full capitalization of Equation 3 yields the proportion of the asset’s ‘true value’ covered by the computations of our flesh-and-blood capitalist. This proportion, which ranges from 0 to 100, is the capitalist’s ‘degree of immortality’ at time t:
Simulation
This isn’t the end of the story, though. As it turns out, the proportion of the asset’s ‘true value’ discounted by the capitalist – and therefore the capitalist’s degree of immortality – depends not only on the number of earning periods n included in the capitalist’s computation, but also on the difference between the discount and the earnings growth rates (r – g). In general, the degree of immortality grows with r and declines with g, so it rises/falls together with the magnitude of (r – g).
These relationships are shown in Figure 1 (where, as before, we assume that the capitalist’s earning predictions are correct). The horizontal axis shows the number of years n whose earnings are being capitalized (the graph caps them at 200, but this number can be made as big as we want). The vertical axis shows the degree of immortality given by the share of ‘true value’ accounted for by the capitalist’s partial computations (0‑100%). The figure shows six curves, representing different values of (r – g) ranging from a low of 0.5% to a high of 5%.
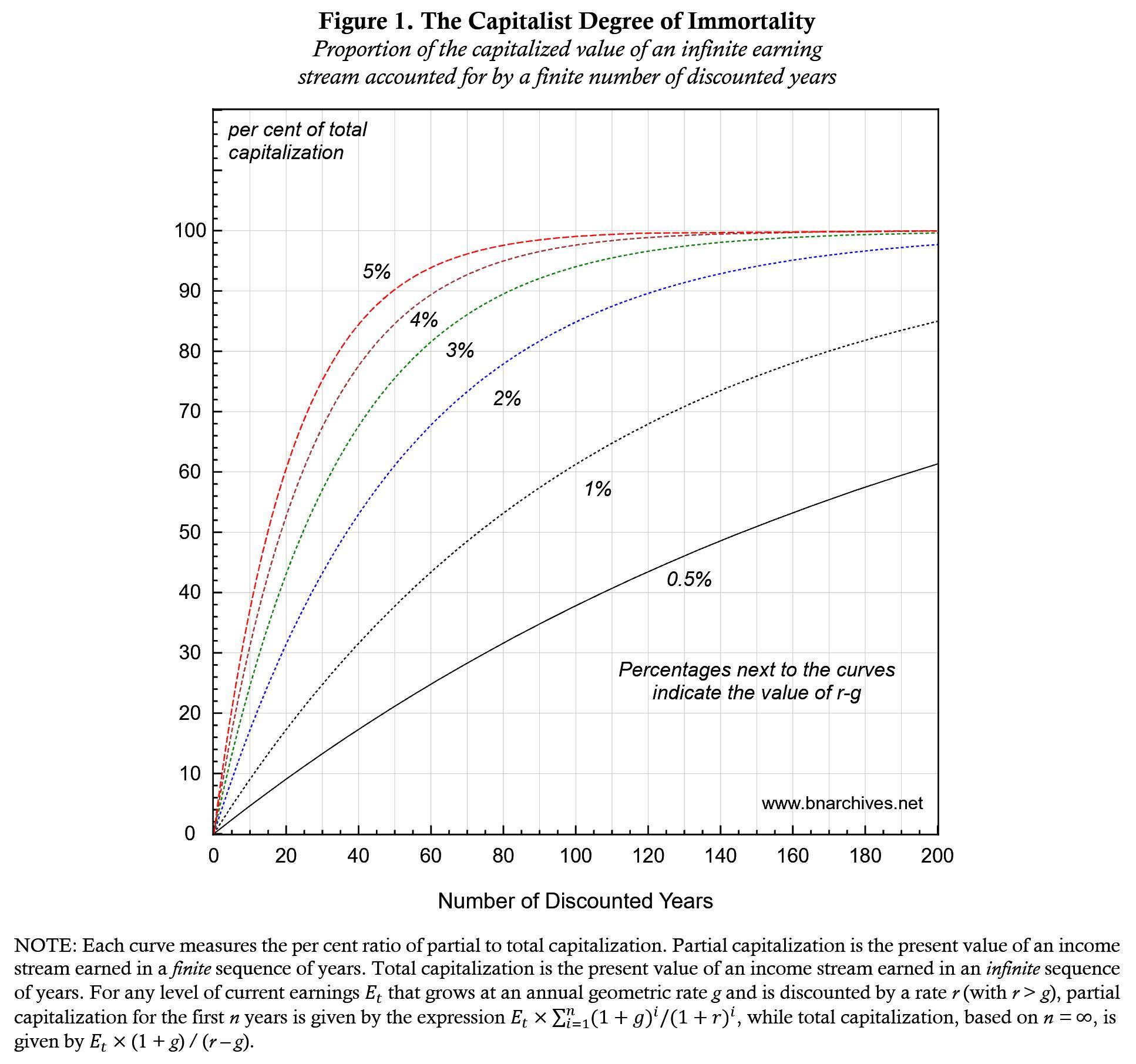
All curves rise from left to right: in other words, for any given (r – g), the greater the included number of earning years, the more accurate the capitalized value of the asset relative to its ‘true value’, and therefore the greater the owner’s degree of immortality. But this degree changes with the magnitude of (r – g). When the discount rate r is significantly bigger than the compounded growth rate of earnings g – for example, when the difference between them is 5% as shown by the top curve – the relative importance of earnings received in the deep future drops perceptibly. Conversely, when the difference between the two rates is small – for instance, 0.5%, as shown by the bottom curve – the relative importance of earnings received in the deep future drops more slowly.
The impact of (r – g) on the degree of immortality is summarized in Table 1. The table shows that when (r – g) = 0.5%, capitalists, even if perfectly prescient, still need 339 years of earning data to have their capitalization reach 80% of ‘true value’ and 485 years to reach 90%. By contrast, when (r – g) = 5%, these same capitalists need only 35 years of data to reach 80% of their asset’s ‘true value’ and 50 to reach 90%.
Bottom Line
Over the past 150 years, S&P 500 earnings per share have grown by a compounded average rate of 4%, while their corresponding discount rate was perhaps twice as high, at 8%. If these rates represent future earnings growth and the rate at which they are being discounted, respectively, they put the (r – g) difference at roughly 4%. With this difference, modern capitalists can achieve 80% immortality with only 44 correctly predicted years of earnings and 90% with a mere 62! A somewhat higher earnings growth and/or lower discount rate would require immortality-hungry capitalists to peer deeper into the future for the same percentages – but even here they could still achieve 80‑90% immortality with roughly a century worth of data, give or take.
Bottom line: eternity has been democratized. It is no longer limited to the hallucinations of Pharaohs, megalomaniac tyrants and mausoleum-bound dictators. Nowadays, all capitalists, actual and aspiring, can get close to it – or so they feel. It is true that dominant capitalists, by virtue of their farther foresight and power to creorder the future, continue to lead the delusional pack. But even retail, mom-and-pop investors can get a little taste of immortality.
No wonder so many people swear allegiance to capitalism. Although the capitalist mode of power often undermines their material interests and hijacks their mind, spirit and autonomy, it gives them a whiff of eternity here and now – and who can resist this quest of Gilgamesh?
Endnotes
[1] Shimshon Bichler and Jonathan Nitzan teach political economy at colleges and universities in Israel and Canada, respectively. All their publications are available for free on The Bichler & Nitzan Archives (http://bnarchives.net). Work on this research note was partly supported by SSHRC.
[2] To be clear, ‘true value’ has nothing to do with truth. It’s simply a convention. This convention, which first emerged in the bourgs of the late Middle Ages, evolved in the twentieth century into a religious-like ritual. Nowadays, this ritual has billions of followers – practically everyone in capitalism is compelled to accept it – but followers, no matter how numerous, are hardly a yardstick for truth (for a detailed analysis, see Nitzan and Bichler 2009: Part III).
References
Kramer, Samuel Noah. 1956. [1981]. History Begins at Sumer. Thirty-Nine Firsts in Man’s Recorded History. 3rd rev. ed. Philadelphia: University of Pennsylvania Press.
Mitchell, Stephen. 2004. Gilgamesh. A New English Version. New York: Free Press.
Mumford, Lewis. 1967. The Myth of the Machine. Technics and Human Development. New York: Harcourt, Brace & World, Inc.
Mumford, Lewis. 1970. The Myth of the Machine. The Pentagon of Power. New York: Harcourt, Brace Jovanovich, Inc.
Nitzan, Jonathan, and Shimshon Bichler. 2009. Capital as Power. A Study of Order and Creorder. RIPE Series in Global Political Economy. New York and London: Routledge.
Zweig, Jason. 2009. Be Inversely Emotional, Not Unemotional. The Wall Street Journal, May 26, pp. 28.
-
Replies
-
-
Jonathan,
This is a very interesting and welcome excursion from current events that doubles as a revelatory application of CasP theory. Are you able to share the underlying data, especially the historical data for r and g (or at least point us to it)? Also, have you undertaken individual analyses of the “epochs” of capitalism sometimes discussed by Blair Fix and others (e.g., golden age, neoliberal era, etc.)? Thanks.
–Scot
-
Are you able to share the underlying data, especially the historical data for r and g (or at least point us to it)?
1. Compounded earnings growth g for the past 150 years is calculated from Robert Shiller’s data.
2. Blair Fix computes the discount rate r for all Compustat firms in the U.S. for 1950-2017, based on the ratio of current profit to current capitalization (i.e. assuming future profits won’t grow), as 6.8%. Since unknown future profits are considered more ‘risky’ than known current profits, we set the discount rate, tentatively, at 8%.
-
Shouldn’t we expect capitalists to already include growing perpetuity of earnings when pricing these kind of assets? If so, Blair’s ‘effective’ discount rate actually corresponds to [r-g]. And if the projected growth rate of earnings is 4%, than the ‘actual’ discount rate [r] is around 12% (instead of 8%). Or am I confusing something?
-
Shouldn’t we expect capitalists to already include growing perpetuity of earnings when pricing these kind of assets? If so, Blair’s ‘effective’ discount rate actually corresponds to [r-g]. And if the projected growth rate of earnings is 4%, than the ‘actual’ discount rate [r] is around 12% (instead of 8%). Or am I confusing something?
Good point, Max.
Let’s hope I don’t screw up the algebra:
1. In his paper, Blair used the simple formula r = K / earnings — i.e., without earning growth.
2. Had he used the formula with compounded earning growth, we would have:
K/E = (1+g)/(r-g) = 0.068
Rearranging the equation, we get:
r = (1 + g(1+0.068))/0.068
If g = 0.04, we get r = 0.153, or 15.3%
-
-
K/E would give us the price to earnings ratio. I think Blair used the inverse formula: r = E/K Adjusted to include compounded growth: E/K = (r-g)/(1+g) = 0.068 g = 0.04 r = 0.068+1.068g = 0.1107 = 11.07%
Thank you Max. Here is the revised version of the paper, posted as a Working Paper on Capital as Power.
-
-
-
K/E would give us the price to earnings ratio. I think Blair used the inverse formula: r = E/K
Thanks for the correction, Max.
Lesson: don’t ignore the seemingly obvious!
-
-
-
- You must be logged in to reply to this topic.