Let’s talk about hype

[jmc]

Part of my research on Netflix is going to test arguments using BN’s concept of hype. Oftentimes, including in my research so far, hype’s place in the capitalization formula has been absorbed into a larger definition of expected earnings. When decomposed into earnings and hype, hype is a short-term scaling factor. It also brings in the effects of herd behavior and human emotion. Didn’t Public Enemy tell us don’t believe the hype?

I’m not sure how many times I will update this thread, but I want to share my experiences using IBES (sometimes styled as “I/B/E/S”), accessed through WRDS. IBES is a Thompson Reuters database that provides histories of financial analyst estimates. Summary histories are available, as well as detailed histories of individual estimates.

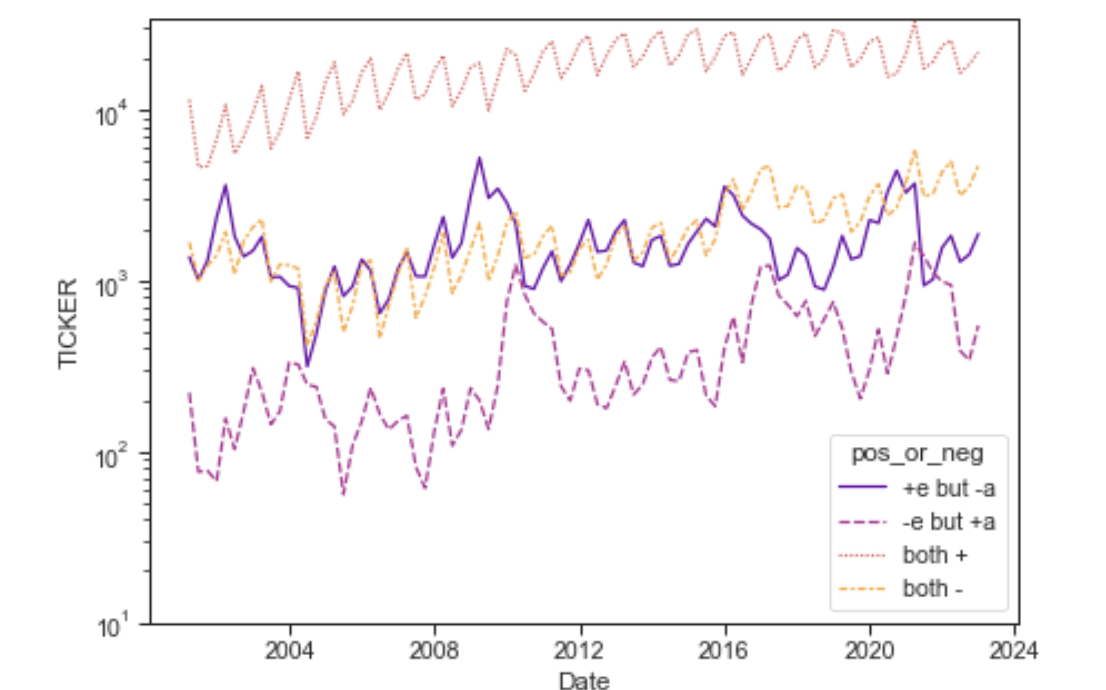
Using the database, it is not hard to replicate BNs measures of hype, which uses EPS. For my paper, I using the detailed history of individual estimates. Thus, each row in the dataset is a single estimate about a specific company. Every estimate is categorized by length of the forecast. The forecast period can be as short as one quarter or longer than ten fiscal years. I’m looking at the forecast period of 4 quarters.

Be sure to download your data with the FPEDATS variable. This enables estimate data to be set to the dates they are estimating, and it makes the comparison to actual values simple.

When actual values are available, my calculation of hype is the natural log of the ratio of an estimate of earnings per share, made four quarters prior, to the actual earnings-per-share value. This is essentially the same thing as BN, but I am taking the log of the ratio to transform the distribution into a more Gaussian shape. Yet taking the log limits this analysis to measures of hype that are composed of two positive numbers. Such a limitation is not as severe as we might think. As I work through this research, I can’t conceptualize (or my math is not good enough) how a ratio with losses would work. Try, for example, to conceptualize what a measure hype would mean when the estimate is positive and the actual is negative, or when both values are negative. When both values are negative, the meaning of the ratio is reversed. A ratio of -3 estimated to -2 actual suggests a pessimistic outlook, but this ratio would produce the same measure of hype as the ratio of 3 estimated to 2 actual, which suggests a positive outlook.

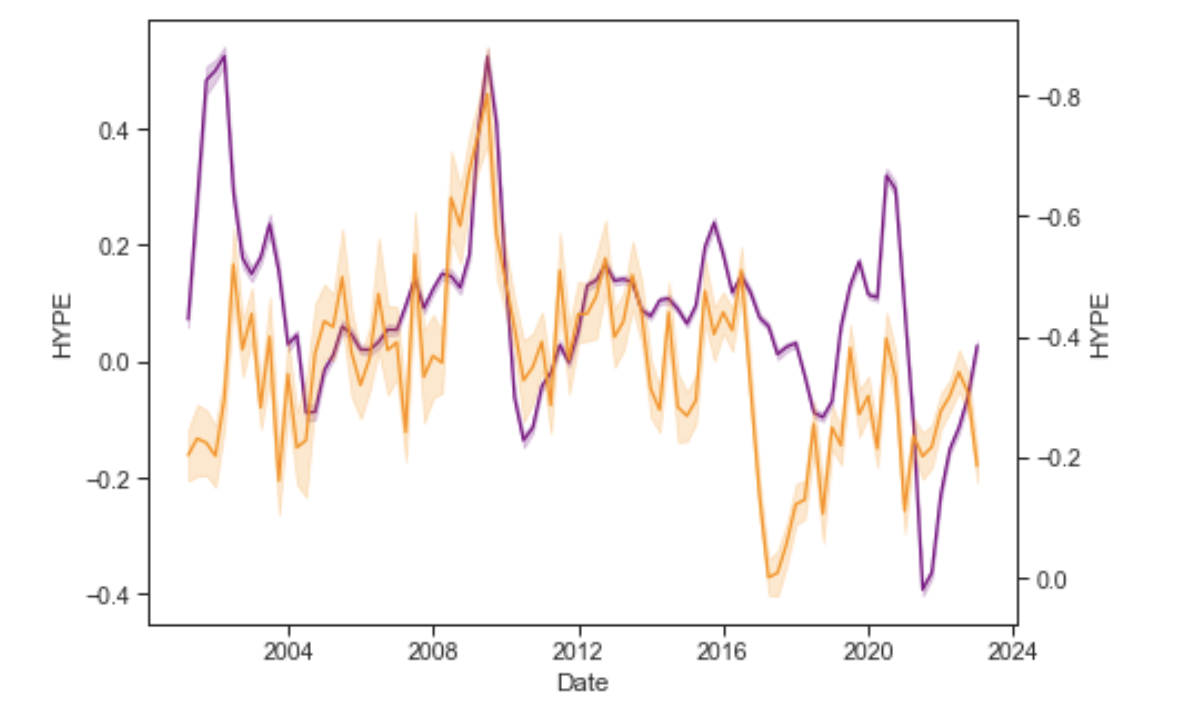
Anyways, here are some graphs to share.

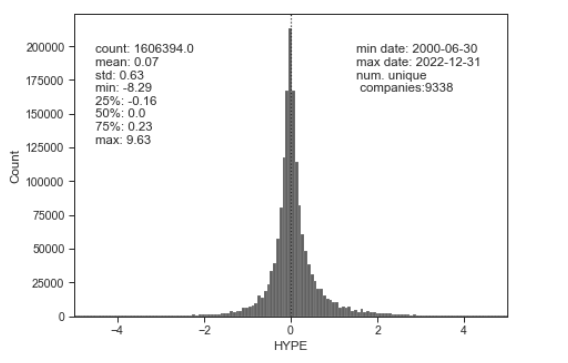
First we have the distribution of all 4-Qtr measures of hype between 2000 and 2022:

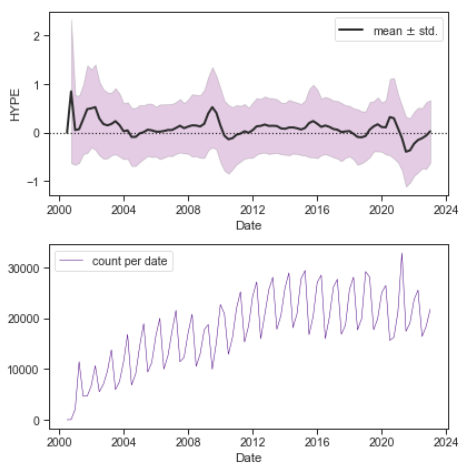
Then we have the mean and standard deviation over the years. One thing I notice is that extreme levels of hype are slightly delayed to the event we would associate it with. The high levels of hype about 2008 financial crisis occur when the rug is pulled from under the estimators. Thus, the big wave of big hype occurs in 2009, when the pre-crash estimates of 2008-Q1 and 2008-Q2 are measured against 2009-Q1 and 2009-Q2.

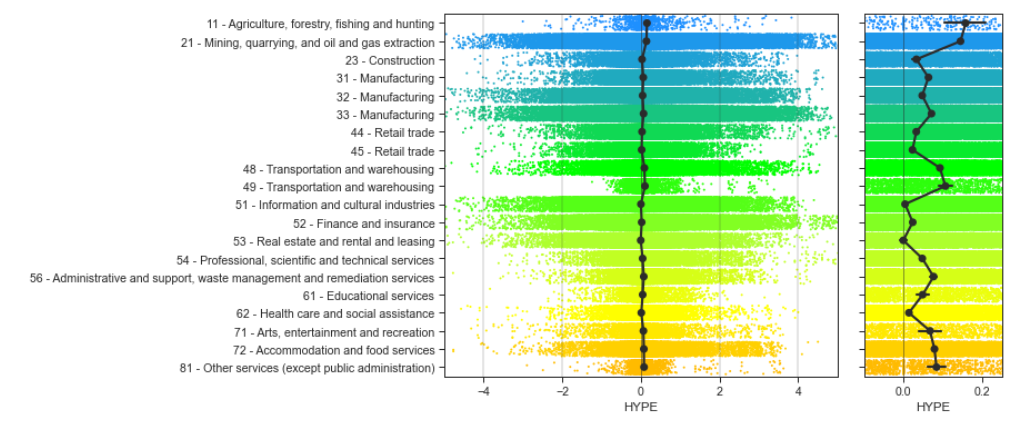
Here are the distributions of hype by NAICS sector (the first 2 digits in often a much larger code).

 

• This topic was modified 1 year, 5 months ago by jmc.

Topic

[Scot Griffin]

Thanks for sharing.

jmc wrote:

When actual values are available, my calculation of hype is the natural log of the ratio of an estimate of earnings per share, made four quarters prior, to the actual earnings-per-share value. This is essentially the same thing as BN, but I am taking the log of the ratio to transform the distribution into a more Gaussian shape. Yet taking the log limits this analysis to measures of hype that are composed of two positive numbers. Such a limitation is not as severe as we might think. As I work through this research, I can’t conceptualize (or my math is not good enough) how a ratio with losses would work. Try, for example, to conceptualize what a measure hype would mean when the estimate is positive and the actual is negative, or when both values are negative. When both values are negative, the meaning of the ratio is reversed. 

Using Excel or equivalent, you can apply if-then tests to convert negative values to absolute values, and you should be able to use if-then tests to write values that tells you whether each value of the numerator and denominator were negative (-1) and/or positive (+1) so you can compare the differences more accurately. At least I think I can imagine graphing that kind of data . . . (maybe using 4 different values mapping to 4 quadrants 1/1, 1/-1, -1/1, and -1/-1, then doing a separate graph that essentially does a quadrant count sorted by implied difference; I don’t know for sure.)

[Blair Fix]

Very interesting research, James. Here are some possible ways to measure hype that would work with negative values:

Nomenclature:

prediction = predicted EPS
actual = actual EPS
abs = absolute value

Hype as the log of absolute value of the prediction error

hype = log( abs( prediction – actual) )

Same thing, but as a fraction of the absolute value of the actual EPS

hype = log( abs( prediction – actual) / abs(actual ) )

With these definitions, ‘hype’ becomes a general measure of prediction error, which is not necessarily what you want. But as Scott notes, prior to taking the absolute values, you could record the sign of (prediction – actual), and then add it back after taking the log. That way, you distinguish between pessimism and hype and also constrain the spread in the measurement.

[jmc]

Thanks, Blair and Scot! Your suggestions already have my head buzzing with simple fixes or proxies.

Here is what I found when I counted by four conditions: both +; both -; +e but -a; -e but +a

The stable majority of data in the dataset have positive estimates and positive actual values. Thousands and hundreds of data per quarter have other states.

I am glad I posted my early research because the condition of negative estimates and negative actual values is an easy fix. I’m going to create a script that will multiply a (-/-) condition by -1, inverting its measure hype and making it consistent with the directional meaning of the BN definition. Below are two series. The purple is (+/+) and the orange is (-/-), with its y-axis inverted.

[Scot Griffin]

Have you considered undertaking a similar analysis of other economic data where a consensus number is tracked, like GDP, PMI, or something like that (if such historical data are available) ? See this economic calendar from NASDAQ, which shows several “consensus” numbers, some side-by-side with the actual numbers announced (especially for days before today, which is still being filled in).

I am just wondering how much of what we are seeing is the hype “signal” versus the macro “noise,”  and, if the two are related, how much macro expectations influence earnings expectations.

 

 

[Author]

Replies