Forum Replies Created
-
AuthorReplies
-
Thank you Scot. I think we are talking past each other. Accountants distinguish between capital invested and the rate of return on the one hand, and the cost of items sold and the markup on the other, such that: 1. rate of return = profit / capital so: profit = rate of return * capital 2. markup = profit / cost of items sold so: profit = markup * cost of item sold. *** In your notes, you say that:
3. profit = rate of return * cost of items sold Unless I made a mistake somewhere, for this last equation to be true, cost of items sold = capital, which normally isn’t the case.
PROFIT AND RATE OF RETURN
I don’t think there is any real disagreement here.
Remember, all I was trying to do was determine whether wages (as a proxy for all input costs) can be viewed as being priced as the discounting of future profits , and they can be. Importantly, my simplified example was limited to a single period (e.g., a fiscal year) in which all capital outlays at the beginning of the period are recouped at the end of the period from the sale of those products along with the profits. So, in my simplified example, capital and costs (or wages, if they are the only costs) are the same thing (addressing your last point).
Yes, things get more complex if we start differentiating between costs that are capitalized expenses (via depreciation) and those that are simple wages, but the discounting never goes away, and that is what matters.
While this insight allows us to view the pricing of the costs incurred by a business as being similar to the pricing of shares of stock for that business, that does not mean they are the same. Not all discounting is capitalization, and I would argue that discounting within a single period, as I’ve done in my simplified model, is not capitalization, which requires discounting into perpetuity, not over a single period. Also, the capital outlays of a business are not the same as the capital outlays of shareholder in that business. The business and its shareholders are investing their capital in different things, at different times, in different markets, over different time periods, all interconnected by a chain of discounting operations assuming different rates of return.
MARKUP
My markup equation is correct.
According to Blair here, markup = profit/sales. (He asserts profit = sales x markup; divide both sides by sales, and you get my equivalent expression).
In Capital as Power (2009), you explicitly define markup as profit/sales. See Fig. 16.3 on page 373 and associated discussion, especially footnote 21 on page 373:

To be fair, in your discussion profit is computed after depreciation, amortization, and income taxes, but my example assumed none of those things applied. Either way, markup = r/(1+r).
Unrelatedly, there seems to be an error in footnote 20 on page 241 of Capital as Power (2009). To achieve a target return of 20%, you need a markup of 16.67%, not 10% (markup equals r/(1+r)), and 16.67% is what you get when you divide $200M in profit by $1.2B in sales (2/12 = 1/6 = 16.67%) on an initial investment of $1.0B.
 Scot, If I understand you correctly, you use r to denote the discount rate, which is distinct from the markup, representing the ratio of profits/revenues. To me, the discount rate r denotes the rate of return (i.e., the rate at which the entity’s assets grow).
Scot, If I understand you correctly, you use r to denote the discount rate, which is distinct from the markup, representing the ratio of profits/revenues. To me, the discount rate r denotes the rate of return (i.e., the rate at which the entity’s assets grow).- Do you share this view? If you do, why is your following expression valid: revenues = Cost (1 + r)
- If you don’t share this view, what do you mean by the discount rate?
Jonathan,
Sorry for the delay in responding.
I view r as both the rate of return (e.g., interest rate) and the discount rate. They must be the same. That’s what makes discounting and compounding inverse, reversible functions of one other: they share the same value of r.
Since profits equal rCosts, revenues must equal Costs(1 + r) such that they yield rCosts after netting out Costs.
December 19, 2022 at 10:04 pm in reply to: Proximity to Legal Authority as a Measure of Power #248755Pieter,
The legislative process often follows the real decision making and serves only to hammer out compromises. As a former PhARMA lobbyist who helped draft Obamacare once told me, “In Washington D.C., you’re either at the table, or you’re on the menu,” which implies the menu has already been decided and the invites have already been sent well before anyone gets seated at the table to officially kick off the legislative process.
As a starting point, it might be easier to invert your inquiry and measure and test the effect of power on legislation. If more capital equals more power, then one would expect to find that dominant capital gets better legislative outcomes at a lower cost, just as it costs them less to raise capital, for example. This kind of approach would allow you initially to focus entirely on financial data, which is much easier to find and less subject/prone to subjective judgments. With that kind of information in hand, it should become more straightforward to develop your taxonomy based on how capital actually asserts its power in the legislative process.
To be clear, the legislature itself is part of the state of capital, so there needs to be a separate inquiry to measure the power of legislators and how the relative gravity of legislators and donors affects the fortunes of legislators. This is a different way to think of Jonathan’s idea of non-linearity: the interaction of multiple centers of capitalist gravity is what creates the appearance non-linearity.
Scot, I think the issue here is not only whether we can write the equations correctly (which often we don’t), but also – and perhaps more so — whether the equations justify our conclusions. You write that:
In a world where the capitalist uses the capitalization equation to set what it will pay for input costs such as wages by discounting its expected profits from future sales, the discount rate used by the capitalist determines (and ensures) the capitalist’s profits.
I think this interpretation is fundamentally wrong. In and of themselves, capitalist expectations of profit, the ex-ante discount rate used to concoct these expectations, and the impact these expectations have on how much they spend on inputs, do not and cannot determine, let alone ensure, actual profits. It seems to me that your claim here is not only unrealistic, but also self-contradictory. Imagine every potential capitalist expecting his/her own profit into existence. This mana-from-heaven magic will make everyone an instant, insatiated capitalist, bring their individual expectations into conflict with each other, and pretty much ascertain that their actual profits will differ from what they expect. In my view, discounted values do not generate power. Instead, it is power that generates discounted values. But we can agree to disagree.
Jonathan,
If you read what I wrote today here and here, you will see I have already back-tracked on my earlier language from yesterday, which you quote above. I have made it clear that equation 6 is an ex ante calculation of forecasted profits, not actual profits, and everything I’ve written previously other than the language you quote supports my claim about the ex ante nature of the calculation, which is clear from the context of its derivation. Hence, my quoted, ill-advised statement regarding “ensuring” actual profits is no longer operative, and you should consider it retracted.
Therefore, please take the time to address what I said here, almost twenty hours after I wrote the language you quote and three hours before you wrote the response quoted above.
If there remains any disagreement, it is not about this: discounted values are determined by discount rates, and discount rates reflect relative power. To me, as I said before, this implies power is confidence in setting the discount rate of a transaction, or, more simply, power is the ability to set the discount rate in the one’s favor. I view either statement as equivalent to confidence in obedience.
What I believe I have shown is that, if I pay you money today in return for your promise of the future payment to me of that same amount of money plus a premium, we can express the relationship between today’s payment and the future premium as discounting. This is true whether today’s payment is provided as a loan, as wages, or as the purchase price of shares, and whether the future premium is in the form of interest, profits, or earnings per share (profits per share less depreciation, amortization and income tax). The future payment of the premium is never guaranteed, but that does not prevent “pricing” what I pay you today by discounting the expected premium you will pay me in the future.
- This reply was modified 3 years ago by Scot Griffin. Reason: removed extraneous language
A related thought:
Just as the future value of something is unknowable, so, too, is the risk. Perhaps the discount rate is really a reflection of relative power and not risk, at least when it comes to certain instances of discounting?
In a world where the capitalist uses the capitalization equation to set what it will pay for input costs such as wages by discounting its expected profits from future sales, the discount rate used by the capitalist determines (and ensures) the capitalist’s profits. See equation 6, below.
Scot, That’s a clever way of presenting your point, but I don’t think the point itself is correct. 1. What capitalists agree to pay workers certainly depends on their profit expectations, but this dependency is not what your equations express.
Jonathan,
Thanks for the comments, which are very helpful. Let me see if I can clarify things, in part by making some things explicit that may not have been.
My equation 6 is ex ante, just like the capitalization equation at page 154 of Capital as Power (2009), and flows from my past experience in setting annual budgets for firms. So, just as capitalists agree to pay for a share of a firm’s stock based on expectations of future earnings, firms budget for input costs (e.g., wages) based on expectations of future profits. I explicitly argue this in my original comment deriving equation 6:
Equation 6 is the same form as the capitalization formula (5) found at the bottom of page 154 of Capital as Power (2009). Thus, wages paid to labor today can be viewed properly as the “risk-adjusted discounted value of expected future earnings” (i.e., Profitst+1), i.e., wages can be viewed as the capitalization of expected profits (or power, if you would prefer). As you’ve said, “capitalization represents the present value of a future stream of earnings: it tells us how much a capitalist would be prepared to pay now to receive a flow of money later.” Capital as Power, at p. 153.
While I agree that firms don’t explicitly employ the discounting formula or a discount rate as part of their annual budgeting process, inherently (mathematically) they do, if they use target mark-ups or profit margins (most capitalist firms use both in some way). That’s what my derivation of equation 6 was intended to show.
2. The discount rate is what investors use to capitalize expected future profits. In your equations, though, r is not the discount rate (the rate of growth of capitalization), but the profit markup over costs (assuming all costs can be expressed as wages).
Actually, the discount rate is a feature of discounting wherever and however applied. There is no single discount rate for everything at every level of the capitalist system, but every instance of discounting has a corresponding discount rate. Thus, the discount rate of a loan extended to a firm can be different than the discount rate the firm applies to expected profits to budget costs (including wages), which in turn can be different than the discount rate capitalists apply to the firm’s expected future earnings. If discounting is used to price money, wages, and equities, the capitalist system is basically a fractal as each level of the system (money, labor, equities) is “self-similar” to the other because each uses discounting to set prices to accumulate power.
Also, the formula for markup is r/(1+r), not 1/r:

3. Moreover, the way you express it, r reflects not the intended markup, but the realized one.
Actually, my intention was to express expected profits, not realized profits, and I said so in my original comment deriving equation 6, as shown above. If we say “expected” instead of “intended,” the same is true of the way you express r in equation 5 at the bottom of page 154 of Capital as Power (2009). Does the future often prove that such expectations were unwarranted? Sure, but that doesn’t make using discounting any less useful for planning/pricing.
The point of discounting is to commensurate two values of the same thing separated in time. The only value we actually ever know is the the present value. The future value is always speculative, which is okay because firms can reduce spending (the present value ) if it appears the future value will fall short of expectations, and they can do so in a manner that adjusts the effective discount rate to make up for missing prior expectations.
Again, budgeting does not explicitly apply discounting, but if the budget includes expectations of profits, it inherently uses discounting.
4. The realized markup – and therefore actual future profit — is neither at the capitalist’s discretion nor knowable beforehand. It depends on how much capitalists will be able to sell in the future, which is anybody’s guess (and the reason why profit forecasters are almost always wrong).
Again, this is true of the capitalization equation at page 154 of Capital as Power (2009). A key difference between capitalization and annual budgeting is that firms plan one fiscal year at a time. It is much easier for firms to forecast revenues/profits accurately on an annual basis than it is for capitalists to price equities into infinity. Also, a firm has the ability to control its expenses, while investors in the firm do not have the ability to control the firm’s earnings.
I recognize that your capitalization equation is somewhat simplified and idealized, but, however expressed, the market capitalization of a firm as calculated by using the last sale price of shares is never accepted by capitalists as an accurate statement of the firm’s value. If that were the case, no shares would transact (every sale of stock is the seller shorting the stock and the buyer going long). This is why financial analysts use things like discounted cash flow analysis to assess what they believe is the actual “intrinsic” share price of a firm.
5. Since capitalists don’t know their actual future profit, they cannot set current wages as a function of that profit.
Nobody knows the future, which is why everybody sets prices (or budgets expenses, or sets a share price objective) based on expectations. Banks make loans knowing there is a risk of default. Firms set annual budgets based on expected profits knowing there is a risk they will not be able to meet expectations. Financial analysts set price objectives using current expectations of future earnings knowing the firm may not meet future expectations.
Anyway, firms set budgets to constrain expenses, including payrolls. If profit targets seem unlikely to be met, the firm can reduce its workforce through layoffs to achieve the desired discount rate (or markup, which is determined by the discount rate).
6. By definition, the wage bill is the product of the wage rate and the level of employment. In general, capitalists control the level of employment — but, in my view, they don’t set the wage rate, which is the result of historical conditions and an ongoing, complex power conflict within the firm and across society. Expected (though not actual) future profit is merely one element of this conflict.
Okay, but each firm determines how large its payroll is. Make of it what you will.
7. For Kalecki, the markup reflects capitalist power. But this reflection is ex post, not ex ante. The discount rate, by contrast, is set ex ante, not ex post. I think it is erroneous to treat them as if they were the same.
During the annual budgeting process, the discount rate and the markup are both set ex ante. That’s just the nature of the budgeting process, the relationship between profits and costs, and the math of discounting. Given an expected markup of m, you can determine the expected discount rate r, even if the concept of “discount rate” and the discounting formula are never explicitly used in the budgeting process.
8. Perhaps it will be useful to try to express your equations in ex-ante terms (rather than ex post), using the discount rate (rather than the markup).
The discounting formula is always ex ante because the future value at time t+1 is not known but expected. Since my equation 6 distinguishes between time t (the present) and time t+1 (the future), I think the suggested work has already been done.
Am I still missing something? The best critique I can see of what I’ve tried to do is that CasP’s capitalization equation is based on a number of simplifying assumptions that I don’t have to make, and the actual math of applying discounted cash flow analysis to determine the intrinsic value of a firm is much more complicated and messy than we are discussing. That’s okay to me because it is enough to be “self-similar,” if the iterative use of discounting over time and space results in capitalism being fractal in nature (which I think it does). Capitalism’s “mega-machine” may just be a self-replicating “nano-bot” called discounting.
Before I finish, we should circle back to the concept that discounting commensurates (equilibrates, really) two values or prices, separated in time, both for the same object. I think this is really important, but I have not had the chance to think through the implications except for how it implies the logic of capitalism is fractal, which may explain why it seems to be so totalizing.
Scot, Come on mate, give me a break. When someone says “it doesn’t add up” that is a colloquial expression. When dealing with arithmetic or math, the potential for any and all operators to be involved is not literally excluded.
But I guess you were just joking. I’m not sure why my point on ““capricious money creation and capricious money destruction” has not been picked up on. Is it “too MMT” or “too Chartalist”? The point is money is fictitious, nominal, formal (choose your preferred term). Obviously, money can be created ex nihilo and destroyed ab nihilo. One thing we need to do (IMHO) is look at the capitalist capture of money creation and money destruction. I don’t think this detracts from CasP but necessarily adds to it. Of course it’s a corporate cartel of powerful capitalists who have captured the formerly state apparatus of money creation and money destruction, not any individual capitalist. When a system runs on chits, it helps to be part of the cartel which prints and shreds the chits, selectively. Or am I wrong? Tell me where I am wrong.
Rowan,
That was more of a riff than a joke, and I certainly did not mean it at your expense. I think CasP on its own terms requires reconsidering the relationship between wages and profits in view of the capitalization equation, which equilibrates the value of one thing at two points in time through multiplication/division, not addition/subtraction.
While modern money is endogenous, it is not fictitious. If it were fictitious, there would be no homelessness, no poverty, etc. The reason money is not fictitious is because human institutions exist to make the consequences of not having money very real. Tim Di Muzio has done the most work on integrating endogenous money theory with CasP analysis. See his Debt as Power, An Anthropology of Money, and The Tragedy of Human Development.
I would also argue that the MMT/neo-chartalist history of money is flat wrong (although certain insights are true). See Colin Drumm’s thesis (I can provide a link). His online courses on money are fascinating and provide a lot of interesting sources throughout history (including Greek tragedies and Shakespeare’s plays).
2. By saying that power is simply ‘the ability to set the discount rate’, you seem to imply that the power of any given entity — me, Musk, JPMorgan Chase — is independent of its (expected) profit. Do you really mean that?
I think I am saying is the opposite.
In a world where the capitalist uses the capitalization equation to set what it will pay for input costs such as wages by discounting its expected profits from future sales, the discount rate used by the capitalist determines (and ensures) the capitalist’s profits. See equation 6, below.
In this sense, profits can be viewed as a “risk premium” accruing to the benefit of the capitalist for (1) providing liquidity to labor, eliminating labor’s risk of survival, while (2) taking on the risk of failing to make a sale. To accept the wages the capitalist offers is to accept the capitalist’s discount rate and provides all the evidence of obedience the capitalist needs to assure its power.
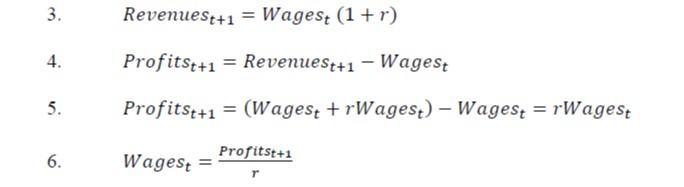
Regarding your first point, I understand and agree that we must distinguish between discount rates set by individual capitalists and the average discount rate of capitalists writ large. I mean, that distinction is the basis for differential accumulation and differential power, right? But is there any reason we cannot apply the insight that wages are just discounted profits in this macro, “average” sense? For example, if wages are just discounted expected future profits, then average hourly wages are necessarily correlated to corporate profits and, by extension, to the SP500 Index, and your Power Index, which is taken from the average/macro level, seems to prove that.
This “firm-wareing” of thought patterns is really, really difficult to overcome. I strongly take the point that prices do not reflect value but rather instantiate power relations. And yet I (still) expect the capitalist book-keeping to add up. So I keep advancing questions that assume that (price) values in the different categories and “departments” (in the Marxian sense) will add up and make arithmetic accounting sense through the economy. Yet there is no reason why they should (add up) under conditions of capricious money creation and money destruction.”
Rowan,
The arithmetic operation you seek is division, not addition. CasP writings obscure this fact by discussing the addition of mark-up to costs to explain the pricing of commodities, but if you choose to model the pricing of all commodities and capital assets as discounting to risk-adjusted present value, which is both reasonable and straightforward to do (I did it on this forum recently), then profits are just the expected value (and reward) for embracing the risk the capitalist discounted previously.
There’s no surplus. There’s no exploitation. There’s no sabotage. There’s just the allocation of risk through discounting, aka “capitalization.” At least that is what the neo-neo-classical economists may say in another 40 years or so, when they realize CasP is an opportunity, not a threat, and incorporate it into their new nonsensical theology. Of course, they won’t say capital is power. They’ll just use the parts of CasP that are useful and jettison the parts that are cryptic (e.g., “power is confidence in obedience”). A better way to say “power is confidence in obedience” that would make it harder for today’s neo-classical “priests” to embrace and suppress CasP is “power is confidence in setting the discount rate,” or, more simply “power is the ability to set the discount rate.”
Demand Deposits, which are the component of M1 most tied to money creation (which is created to spend, not save), is probably a better series than all Deposits. Similarly, you probably want Loans and Leases in Bank Credit, which excludes treasuries, mortgage-backed securities, and other securities held by banks, instead of all Bank Credit.
My hypothetical may be wrong. See, this paper from Richard Werner.
money is by definition on the liabilities side of the bank’s balance sheet
There are two kinds of ‘money’ in operation here. One is ‘credit money’ which sits on the liabilities side. The second is ‘currency money’ (which originates from a central bank loan or from the bank owners equity) and it sits on the assets side (reserves). Let’s just agree to call it currency for now. As I understand it, the argument (by Keen, et al.) is as follows – The books need to be kept balanced at any time and after each monetary occurrence by a double-entry procedure: 1: New loan [+ Asset (loan)]–>new deposit [+ Liabilities] 2: Deposit leaves the bank [- Liabilities]–> currency leaves the bank [- Assets (reserves)] 3: interest paid on the loan: currency flows to the bank [+ Assets (reserves)] –>profit registered for owners [+ Liabilities (equity)] 4: principal returns [- Assets (loan “write-off”)]–>currency returns to the bank [+ Assets (reserves)] This is a simple example involving all of the recorded credit money leaving the bank (so all of the currency corresponding to the loan/deposit figures needs to be employed). But a similar procedure can be described for the extreme counter example (all recorded credit money stays in the bank, so no need for currency transfers). In my opinion, this is the only explanation that makes sense. Registering the returned principal as a net asset would violate accounting rules since it would register twice on the asset side (as currency and as “write-off loan money”), resulting in the need for recording a third monetary occurrence (crediting equity out of the blue) with no corresponding double-entry registration. Or else the books will not stay balanced.
Thanks for the explanation, Max. You’ve given me something I can follow up on directly.
When I refer to money, I’m referring to M1 and M2 monetary aggregates. M1 includes the currency components (FRED series CURRSL). As you can see from Table H.6, currency is about 10% of M1 these days, but that is due to a recent change in the definition of M1 to include savings accounts. Historically, currency was 20-30% of M1 until 2000, when it jumped to 40-50%.
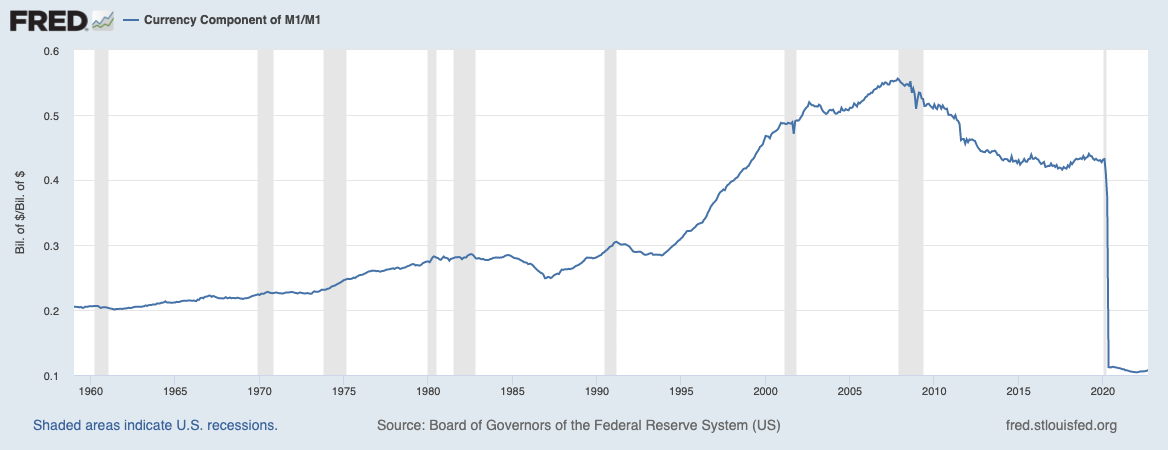
Loan proceeds need not be converted into currency, and most times they are not. Interbank transfers, whether accomplished via physical check or electronic transfer, do not require an exchange of currency, just the exchange of liabilities (deposits).
Bank reserves are not considered part of M1 or M2 and so are not considered money, although they are considered part of the monetary base (see Table H.6). It is my understanding that reserves do not circulate. Maybe currency and reserves are distinct things?
Are you aware of an accounting rule for determining whether a “monetary event” has occurred? I ask this because, as late as 2015, economists like Richard Werner were conducting experiments to empirically test how money is created, and he concluded the “dominant” theory of loanable funds was incorrect and the fringe credit-theory of money was correct. How could the loanable funds theory even be considered viable if the accounting rules were clear on how to treat payments of principal?
The problem is that the balance sheet reflects its current state, not its history. It should be possible to construct balance sheets of a non-bank firm and a bank that are identical at the time the loan is made. For example, imagine the non-bank firm is a store or a brokerage firm that maintains accounts for its customers on its books, which allow it to track store credits, etc.
Using the notation Assets-Liabilities-Equity, at time T0, the nonbank firm’s balance sheet is 100-0-100, and the bank’s balance sheet is 0-0-0. At time T1, both extend a loan, resulting in identical balance sheets of 100-100-0 (the non-bank debits $100 from its assets, credits that $100 to its customer’s account, and credits as a firm asset the customer’s IOU for $100; the bank just credits $100 to both assets and liabilities). At time T2, the debtors repay the loan in full at 10% interest ($10). The non-firm’s balance sheet should be 110-0-110 (I think, if the hypothetical as constructed is logically sound), is the bank’s balance sheet 10-0-10? (NOTE: I don’t think equity is credited; it is calculated by subtracting assets from liabilities).
Thanks for your help in working through this. I appreciate it.
- This reply was modified 3 years, 1 month ago by Scot Griffin. Reason: Clarified non-bank hypothetical
- This reply was modified 3 years, 1 month ago by Scot Griffin. Reason: added language to distinguish between reserves and currency
I once used Emmanuel Saez’s data along with IRS data to calculate debt-to-wage ratios for the top decile and the bottom 90%. (I avoided using BEA data due to its use of fictitious imputations.)
Here is a link to the BEA’s NIPA Handbook explaining what NIPA’s Corporate Profits data reflect. I agree with Jonathan that NIPA does not disaggregate profits in the way you would like.
Also, accounting rules allow things like software to be capitalized, i.e., to be treated as capital goods or fixed capital, and depreciated over time. This is why I think of fixed capital as a “stupid accounting trick” that delays certain expenses from hitting the income statement, smoothing profits and losses over time. It is a fiction born out of fairness, though. A manufacturer cannot make or sell any products until it builds a factory. Accounting rules allow the manufacturer to account for the expense of building the factor on its cash flow statement while deferring the recognition of that expense on the income statement on a pro rata basis over the useful life of the factory, which is usually 20-30 years. Capital expenses for things like software may have a useful life (reflected in the depreciation schedule) of only 1-2 years.
We received the following question from an economics professor:
Dear Jonathan, […] I come from “mainstream econ” but, with time, I have become increasingly critical of the mainstream dogma. I enjoyed reading your book “Capital as Power” and I have a question related to your “inflation as redistribution” graphs on pages 371 and 373. The recent “Nobel prize” in Economics seems to emphasize banks’ role as intermediaries who merely receive money from depositors and channel it to borrowers. The reality is that they are producers of purchasing power (as noted by Schumpeter). I wonder whether one can think of money creation as redistribution in much the same way as you thought of inflation as redistribution in the above-mentioned graphs. In other words, is it possible to plot your differential markup (resp., the ratio of corporate earnings per share to the wage rate) together with some measure of money creation? The question, of course, is whether these series are positively correlated. Is this a sensible question? If so, would your theory be able to shed some light on the relationship between money creation and redistribution? Thanks.
Here is a tentative reply: 1. For simplicity, let’s assume that: bank profits = lending rate * loans – deposit rate * deposits – cost of operation 2. If loans and deposits move more or less in tandem, and if the cost of operation is relatively stable, bank profitability will depend mostly on the lending-deposit spread. 3. We haven’t studied this question empirically, but my hunch is that the lending-deposit spread could very well be negatively correlated with money growth. 4. If conjecture 3 is correct, it follows that when the money supply grows, bank profits (as well as their share in overall profit) will expand due to the growth of money but contract due to the accompanying compression of the spread, leaving the net effect uncertain. It will be interesting to see someone examining this question empirically for a number of countries.
When it comes to money creation through bank loans, we should probably be talking about the distribution of power, not the redistribution of income.
Consider a bank “loan” in isolation. Banks do not lend money, they create money in exchange for the debtor’s promise to pay that money plus interest to the bank at a later time.
When the debtor pays off the “loan,” the interest is treated as profit, but how is the “principal” that has been “repaid” treated? Is it extinguished along with the debtor’s legal obligation to pay the principal, or does it accrue as a “return” of the bank’s capital on the assets side of its balance sheet (i.e., is the capital of the loan obligation transformed into reserves as principal is repaid)? To calibrate, principal payments made on loans extended by non-banks are treated as the return of capital and carried as an asset but not taxed as income.
Steve Keen and MMTers argue that since the repayment of bank debt destroys money, the only thing the bank has on the assets side of the balance sheet when the debt is paid is the interest, which as taxable as profits.
While I agree that paying bank debts destroys money, money is by definition on the liabilities side of the bank’s balance sheet, so the fact that “money is destroyed” does not tell us anything about what happens on the assets side of the balance sheet.
The way I understand Steve’s argument, it is the double-entry nature of accounting that enforces destruction of the “repaid” capital on the assets side of the balance sheet. The problem with his argument, and the likely reason for the continued existence of the empirically false loanable funds theory of banking (which claims banks are merely intermediaries who shuttle money from depositors to debtors), is the accounting rules and tax laws treat the stated amount of principal of the debt obligation as if it were capital that existed at the time of the bank loan such that the the payment of principal is treated as a return of the bank’s capital and not subject to taxation. In other words, when it comes to bank loans and their repayment, there is more than one accounting rule in operation.
I am not an accountant, but I have worked closely with accountants over the years in preparing financial reports for the SEC and investors, and I have made a serious effort to find relevant accounting rules that support Steve’s argument, to no avail. I have also asked him and anyone who knows to point me to applicable accounting rules, but they have not been able to do so.
If such a rule existed, it should be easy to find. Why? Because the rules would distinguish between two types of loans: (1) bank loans that did not involve the transfer of existing funds; and (2) all loans by non-banks, which require the transfer of existing funds. To the extent such accounting rules exist (and they do, at least with respect to how to mark-to-market the value of the loan), they treat the repayment of principal the same, i.e., there’s no rule that says banks must write-off/destroy the principal as it is repaid (even as the legal obligation of repayment is debited), and, if there were, the market value of any bank loan for accounting purposes must always be zero (even though the legal obligation to pay the principal plus interest remains). Indeed, absent the likelihood of default, accounting rules recognize the unpaid principal amount of bank loans held for their duration as their market value on the books. Accounting rules treat bank loans held for sale differently because the secondary market (e.g., for home mortgages) prices each individual loan at, below, or above the unpaid principal amount.
The existence of secondary markets for bank loans and credit collection agencies further argue against the notion that the end-value of repaid principal is null.
If principal payments accrue as the return of capital, bank money creation results in the banks’ “immaculate accumulation” of capital.
If principal payments somehow evaporate into nothingness (if so, I really would like somebody to explain how that is the case; I want to be proven wrong), it might be informative to spend some time with the specifics of how banks report income. If BofA and Wells Fargo are indicative of the banking industry as a whole, all US banks report income as “net interest income” and “non-interest income.” Net interest income nets out interests paid on deposits and therefore reflects the “spread” you discuss above. You will see that non-interest income is on the same order of magnitude for both BofA and Wells Fargo.
Regardless, instead of trying to measure whether money creation redistributes income, it would probably be easier to consider annual debt service as a percentage of GDP and/or annual money creation relative to annual debt service. NOTE: It would be better to consider net debt service (debt service minus interest payments), but I have not been able to figure out how to isolate interest payments from the Fed Flow of Funds data.
-
AuthorReplies
